Глава 7. Матричные преобразования
Содержание главы
- Линейные преобразования
- Аффинные преобразования и выход за их пределы
- Camera Transforms
В моём описании преобразований в Главе 2 «Преобразования и анимация» и Главе 3 «Вращение, заданное осью и углом поворота» был опущен один из классов, производный от Transform3D (трёхмерное преобразование). Этим таинственным классом был MatrixTransform3D (трёхмерное матричное преобразование). Этот класс обладает гибкостью, достаточной для осуществления стандартных преобразований перемещения, масштабирования и поворота (и не только их). Естественно, по мере увеличения гибкости, снижается простота использования. У этого класса есть только одно свойство — Matrix (матрица) типа Matrix3D, представляющего собой структуру, имеющую 16 собственных свойств, доступных для чтения и записи. В XAML можно задать значения этих свойств либо по отдельности, либо описав матрицу целиком одной строкой из 16 чисел.
Если вы полагаете, что для ваших нужд вам вполне достаточно стандартных преобразований перемещения, масштабирования и поворота, то можно полностью избежать применения структуры Matrix3D. Но понимание её роли в программировании трёхмерной графики открывает путь к ряду продвинутых техник.
Структура Matrix3D реализует математическую сущность, которой примерно в середине XIX столетия английским математиком Джеймсом Джозефом Сильвестром (1814-1897) было дано имя «матрица». Тот факт, что графические преобразования зачастую выражаются в виде матриц, объясняется тем, что матричная алгебра позволяет легко оперировать такими преобразованиями. Например, составные преобразования эквивалентны умножению матриц, а обратные преобразования — обращению матриц. Предполагаю, что, получая образование, вы уже встречались с матрицами, но, на случай если вы их слегка подзабыли, я приведу краткий обзор.
Существуют разные способы подразделения преобразований на категории. И по мере того, как эти категории будут нам встречаться, я дам им определения. В своём рассказе о матрицах в этой главе я сперва сфокусируюсь на линейных преобразованиях, затем на аффинных и, наконец, на неаффинных. Если поначалу покажется, что я в своём изложении что-то опускаю, пребывайте в уверенности, что это будет рассмотрено в своё время.
Линейные преобразования
В математике функция f называется линейной, если для переменных x и y и константы k справедливы следующие соотношения:
f(x + y) = f(x) + f(y)
f(kx) = kf(x)
Применительно к трёхмерной графике, такая функция f вполне может выражать преобразование, а значениями переменных x и y в этом случае будут скорее не числа, а точки или векторы в трёхмерном пространстве. На самом деле, легче мыслить в терминах векторов, нежели точек, потому что векторы можно складывать или умножать на константу, а для точек эти понятия не имеют смысла.
Итак, с математической точки зрения преобразование путём масштабирования является линейным. И преобразование путём поворота — линейно. Другие виды преобразований (например, такое как сдвиг или скос) тоже линейны. Однако перемещение — в каком-то смысле, простейшее из всех преобразований — не является линейным. К счастью, эта небольшая проблема влечёт за собой решение, сулящее и другие выгоды.
Обзор матричной алгебры
Матрица — это прямоугольная таблица чисел с фиксированным количеством строк и столбцов. Матрица 3×4 имеет три строки и четыре столбца.
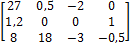
При записи матрицы, таблица чисел заключается в квадратные скобки (наряду с которыми могут использоваться и круглые, а также двойные вертикальные линии). Нередко для обозначения матриц используются жирные заглавные буквы латинского алфавита (например, A). Числа, составляющие матрицу, называются элементами матрицы. Иногда говорят, что матрица содержит ячейки. Отдельно взятый элемент матрицы записывается с двумя индексами, например aij, где i — номер строки, а j — номер столбца. Чаще всего эти индексы отсчитываются от единицы, а не от нуля. Например, в вышеприведённой матрице, a11 — это элемент, находящийся в левом верхнем углу, а a34 — элемент в нижнем правом углу.
Две матрицы можно складывать или вычитать одну из другой путём сложения или вычитания соответствующих элементов (то есть поэлементно). Можно умножить матрицу на скаляр (одно число) путём умножения каждого элемента на этот скаляр.
Более интересной операцией является умножение двух матриц. Предположим, что A и B — это две матрицы с элементами aij и bij, а матрица C с элементами cij — это их произведение:
A × B = C
Произведение определено только в том случае, если число столбцов матрицы А равно числу строк матрицы В. При этом матрица-произведение C имеет столько же строк, сколько у матрицы A, и столько же столбцов, сколько у матрицы B. А каждый элемент матрицы C может быть рассчитан по следующей формуле (в которой N — это число столбцов матрицы A или строк матрицы B):
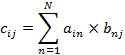
Большая греческая буква «сигма» обозначает суммирование, где n принимает значения от 1 до N. На самом деле, умножать матрицы на практике гораздо легче, чем в теории. Возьмём следующие три матрицы:
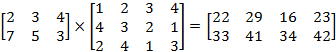
Я уже заполнил элементы матрицы-произведения. Как видите, количество столбцов первой матрицы (три) совпадает с количеством строк второй матрицы. Матрица-произведение содержит столько же строк, сколько первая матрица (две), и столько же столбцов, сколько вторая (четыре).
Начните с первой строки первой матрицы, содержащей числа 2, 3 и 4. Поверните её в уме так, чтобы она стала вертикальной. Поставьте её рядом с первым столбцом второй матрицы (числа 1, 4 и 2). Перемножьте соответствующие числа и сложите результаты: 2, умноженное на 1, плюс 3, умноженное на 4, плюс 4, умноженное на 2, что равняется 22. Это число помещается на пересечении первой строки и первого столбца матрицы-результата. Продолжайте выполнять описанные операции, используя первую строку первой матрицы и, последовательно, второй, третий и четвёртый столбцы второй матрицы, чтобы заполнить первую строку матрицы-результата. Теперь возьмите вторую строку первой матрицы: числа 7, 5 и 3. Снова, поверните её набок и перемножьте с первым столбцом второй матрицы: 7, умноженное на 1, плюс 5, умноженное на 4, плюс 3, умноженное на 2, что равняется 33. Это — результат для первого столбца второй строки. Теперь продолжайте поэлементно умножать вторую строку первой матрицы на второй, третий и четвёртый столбцы второй матрицы, чтобы заполнить оставшиеся столбцы второй строки матрицы-результата.
Вообще, умножение матриц некоммутативно. Другими словами, произведение A × B не обязательно равно B × A. Это очевидно из предыдущего примера, потому что число столбцов первой матрицы должно быть равно числу строк второй матрицы, а это правило не будет выполняться, если мы поменяем матрицы местами. Но, даже если бы матрицы были квадратными (то есть имели бы одинаковое число строк и столбцов), операция умножения матриц, как правило, не будет коммутативной. Тем не менее, умножение матриц ассоциативно: в произведении A × B × C не важно, какое умножение произвести в первую очередь. Умножение матриц также является дистрибутивным относительно сложения:
A × (B + C) = A × B + A × C
Матрицы и преобразования
Точка в трёхмерном пространстве, задаваемая координатами (x; y; z), может быть представлена в виде матрицы 1×3:
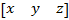
Линейное преобразование может быть представлено в виде матрицы 3×3:
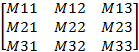
Я записал элементы этой матрицы, используя имена свойств, определённых для структуры Matrix3D, которые удобно указывают на номер строки и столбца. Преобразование — это умножение точки в пространстве на матрицу 3×3.
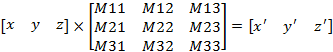
Исходная точка (x; y; z) преобразуется в новую точку (x'; y'; z') согласно следующим формулам, вытекающим из правила умножения матриц:
x' = M11 • x + M21 • y + M31 • z
y' = M12 • x + M22 • y + M32 • z
z' = M13 • x + M23 • y + M33 • z
Можно сказать, что преобразование сопоставляет точке (x; y; z) точку (x'; y'; z').
(Должен отметить, что в некоторых книгах, посвящённых компьютерной графике, это умножение матриц показано немного по-другому: строки и столбцы матрицы преобразования меняются местами, что требует представления преобразуемой точки в виде матрицы-столбца 3×1, который помещают справа от матрицы преобразования при записи произведения. И, хотя такая запись имеет некоторые преимущества, я буду придерживаться правила, вытекающего из имён свойств структуры Matrix3D).
Преобразование, представленное этой матрицей 3×3, называется линейным преобразованием, потому что в каждую формулу входят лишь произведения констант на координаты точки x, y, и z, и это удовлетворяет критериям математической линейности. Я хочу, чтобы у вас сложилось хорошее понимание формул для вычисления новых координат (x', y' и z'). Так, чтобы, видя матрицу 3×3, вы понимали, что её первый столбец содержит множители для вычисления координаты x', второй — для координаты y', а третий — для координаты z'.
Можно посмотреть на это ещё под одним углом: предположим, что (x; y; z) — это не точка, а вектор: (x; y; z). Три столбца матрицы преобразования тоже можно представить как векторы: (M11; M21; M31), (M12; M22; M32) и (M13; M23; M33). В этом случае, преобразованные координаты x', y' и z' — это значения трёх скалярных произведений вектора (x; y; z) с тремя составляющими матрицу векторами-столбцами:
x' = (x; y; z) ∙ (M11; M21; M31)
y' = (x; y; z) ∙ (M12; M22; M32)
z' = (x; y; z) ∙ (M13; M23; M33)
Такой подход к интерпретации преобразований является весьма полезным.
Использование класса MatrixTransform3D (трёхмерное матричное преобразование)
При создании нового объекта типа MatrixTransform3D, его свойство Matrix содержит создаваемый по умолчанию объект типа Matrix3D, выражающий матрицу, значения, лежащие на главной диагонали которой равны единице:
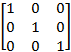
Эта матрица известна под названием единичной, и именно такой объект создаёт конструктор без параметров структуры Matrix3D. Единичная матрица — это матрица, эквивалентная числу 1. Умножение любой матрицы на единичную не приводит ни к каким изменениям. Формулы преобразования, связанные с единичной матрицей, просты:
x' = x
y' = y
z' = z
Вы, наверное, знаете, что у структуры её конструктор по умолчанию (конструктор без параметров) всегда задаёт нулевые значения для всех полей этой структуры, поэтому может показаться немного странным, что результатом работы конструктора без параметров структуры Matrix3D является единичная матрица, некоторые свойства которой равны 1. На самом деле, внутренние значения всех полей структуры Matrix3D равны нулю, но свойства M11, M22 и M33, очевидно, добавляют единицу к значениям, хранящимся в связанных с этими свойствами полях.
Элемент MatrixTransform3D можно использовать там же, где вы используете элементы TranslateTransform3D, ScaleTransform3D или RotateTransform3D. Ниже представлен пример, в котором элемент Matrix3D помещён в элемент, соответствующий свойству MatrixTransform3D.Matrix:
<MatrixTransform3D>
<MatrixTransform3D.Matrix>
<Matrix3D M11="1" M12="0" M13="0"
M21="0" M22="1" M23="0"
M31="0" M32="0" M33="1" />
</MatrixTransform3D.Matrix>
</MatrixTransform3D>
В этой разметке представлены свойства структуры Matrix3D с их заданными по умолчанию значениями, наглядно расположенными в виде массива. В приведённом далее содержимом файла LinearTransformExperimenter.xaml можно найти подобный элемент Matrix3D, с которым можно поэкспериментировать.
LinearTransformExperimenter.xaml
<!-- ==============================================================
LinearTransformExperimenter.xaml (c) 2007 by Charles Petzold
============================================================== -->
<Page xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"
xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
WindowTitle="Linear Transform Experimenter"
Title="Linear Transform Experimenter">
<DockPanel>
<!-- Scrollbars to view object from different sides. -->
<ScrollBar Name="horz" DockPanel.Dock="Bottom" Orientation="Horizontal"
Minimum="-180" Maximum="180"
LargeChange="10" SmallChange="1" />
<ScrollBar Name="vert" DockPanel.Dock="Right" Orientation="Vertical"
Minimum="-180" Maximum="180"
LargeChange="10" SmallChange="1" />
<Viewport3D>
<ModelVisual3D>
<ModelVisual3D.Content>
<Model3DGroup>
<GeometryModel3D>
<GeometryModel3D.Geometry>
<!-- House: front, back, left roof, left,
right roof, right, bottom. -->
<MeshGeometry3D
Positions=
" 0 1 1, -0.5 0.6 1, 0.5 0.6 1,
-0.5 0 1, 0.5 0 1,
0 1 -1, 0.5 0.6 -1, -0.5 0.6 -1,
0.5 0 -1, -0.5 0 -1,
0 1 -1, 0 1 1,
-0.5 0.6 -1, -0.5 0.6 1,
-0.5 0.6 -1, -0.5 0.6 1,
-0.5 0 -1, -0.5 0 1,
0 1 1, 0 1 -1,
0.5 0.6 1, 0.5 0.6 -1,
0.5 0.6 1, 0.5 0.6 -1,
0.5 0 1 0.5 0 -1,
0.5 0 1, 0.5 0 -1,
-0.5 0 1, -0.5 0 -1"
TriangleIndices=
" 0 1 2, 1 3 2, 2 3 4,
5 6 7, 6 8 7, 7 8 9,
10 12 11, 11 12 13,
14 16 15, 15 16 17,
18 20 19, 19 20 21,
22 24 23, 23 24 25,
26 28 27, 27 28 29" />
</GeometryModel3D.Geometry>
<GeometryModel3D.Material>
<DiffuseMaterial Brush="Cyan" />
</GeometryModel3D.Material>
<GeometryModel3D.BackMaterial>
<DiffuseMaterial Brush="Red" />
</GeometryModel3D.BackMaterial>
<!-- Matrix transform. -->
<GeometryModel3D.Transform>
<MatrixTransform3D>
<MatrixTransform3D.Matrix>
<Matrix3D
M11="1" M12="0" M13="0"
M21="0" M22="1" M23="0"
M31="0" M32="0" M33="1" />
</MatrixTransform3D.Matrix>
</MatrixTransform3D>
</GeometryModel3D.Transform>
</GeometryModel3D>
<!-- Light sources. -->
<AmbientLight Color="#404040" />
<DirectionalLight Color="#C0C0C0" Direction="2, -3 -1" />
</Model3DGroup>
</ModelVisual3D.Content>
</ModelVisual3D>
<!-- Camera. -->
<Viewport3D.Camera>
<OrthographicCamera Position="0 0 4"
LookDirection="0 0 -1"
UpDirection="0 1 0"
Width="4">
<OrthographicCamera.Transform>
<Transform3DGroup>
<RotateTransform3D>
<RotateTransform3D.Rotation>
<AxisAngleRotation3D Axis="0 1 0"
Angle="{Binding ElementName=horz,
Path=Value}" />
</RotateTransform3D.Rotation>
</RotateTransform3D>
<RotateTransform3D>
<RotateTransform3D.Rotation>
<AxisAngleRotation3D Axis="1 0 0"
Angle="{Binding ElementName=vert,
Path=Value}" />
</RotateTransform3D.Rotation>
</RotateTransform3D>
</Transform3DGroup>
</OrthographicCamera.Transform>
</OrthographicCamera>
</Viewport3D.Camera>
</Viewport3D>
</DockPanel>
</Page>
Содержащийся в файле код отображает простой трёхмерный домик, размещённый на координатной плоскости XY. Ширина этого домика составляет одну единицу, высота — тоже одну единицу, глубина — две единицы, а оси X и Z обе проходят под центром домика. Ортографическая камера (объект OrthographicCamera) направлена на фасад дома так, что сперва виден только его торец, но, при помощи двух полос прокрутки, можно подобрать иную, лучшую, точку обзора.

Наиболее познавательным было бы загрузить этот файл LinearTransformExperimenter.xaml в программу XamlCruncher или подобную ей и поэкспериментировать со свойствами элемента Matrix3D. Три элемента, расположенных на диагонали матрицы, — M11, M22 и M33 — управляют масштабированием в направлениях X, Y и Z. Задание значений для этих свойств имеет такой же эффект, как и задание значений для свойств ScaleX, ScaleY и ScaleZ объекта ScaleTransform3D. Если установить все три эти свойства равными 5, то домик увеличится настолько, что камера окажется внутри его, и вы увидите его внутреннюю поверхность, окрашенную в красный цвет.
Также можно вращать фигуру вокруг осей X, Y и Z. Поворот вокруг оси Z требует следующей матрицы преобразования:
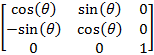
Формулы преобразования имеют следующий вид:
x' = x • cos(θ) – y • sin(θ)
y' = x • sin(θ) + y • cos(θ)
z' = z
Эти формулы подобны формулам для получения окружности, с которыми мы встречались в предыдущей главе. Для поворота на 30 градусов вокруг оси Z потребуются следующие значения:
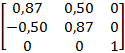
И вот результат (если смотреть, немного сбоку):

Поворот вокруг оси X выражается следующей матрицей:
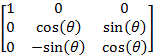
Наконец, вращение вокруг оси Y задаётся так:
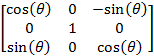
Обратите внимание, что в каждой из этих базовых матриц поворота, координаты, соответствующие оси поворота, не затрагиваются. Например, матрица, задающая поворот вокруг оси Y, оставляет неизменными все значения y.
Поворот вокруг произвольной оси — вектора (x; y; z) — задаётся более громоздко, но если такой вопрос у вас возник, то приведём матрицу и для него (для упрощения синтаксиса скобки вокруг операндов тригонометрических функций опущены):
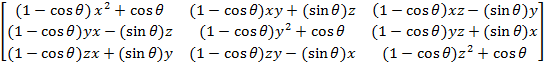
Имейте ввиду, что значения x, y и z в этой матрице являются координатами вектора, задающего ось вращения, а не вращаемой точки. Если задать для x и y нулевые значения, а для z — единичное (что означает поворот вокруг оси Z), то матрица упростится и будет соответствовать приведённой выше. То же самое относится и к другим базовым единичным векторам (ортам).
Пока вы ещё не увидели ничего такого, чего бы вы не смогли сделать при помощи объектов ScaleTransform3D или RotateTransform3D, однако только объект MatrixTransform3D может задавать преобразование сдвига (также называемого скосом). В процессе этого преобразования, прямые углы становятся острыми или тупыми. Например, попробуйте использовать следующую матрицу:
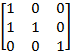
Это — практически единичная матрица. Единственное отличие — в ещё одном равном единице элементе. Так что формула для x' принимает вид:
x' = x + y
Для точек, находящихся выше плоскости XZ, по мере роста высоты над плоскостью, значения координаты x возрастают (точки смещаются в сторону положительного направления оси X). В то же время точки, находящиеся ниже этой плоскости, смещаются в сторону отрицательного направления оси X вследствие уменьшения значения координаты x по мере увеличения расстояния до плоскости XZ. Домик наклоняется:

Можно сдвигать домик в самых разных направлениях, задавая отличные от нуля значения для нулевых элементов матрицы. Вот, например, такой вариант:
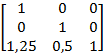
Значения z оставлены неизменёнными, а значения x и y смещаются в зависимости от значения z:
x' = x + 1,25 z
y' = y + 0,5 z
Например, для множества точек, у которых координата z равна 1 (что соответствуют плоскости, проходящей через фасад домика), формулы преобразования примут вид:
x' = x + 1,25
y' = y + 0,5
И вот как это выглядит:
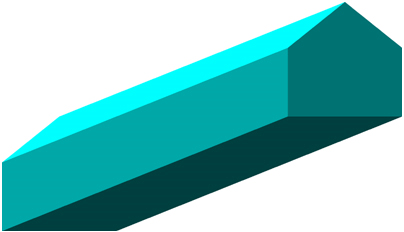
Постарайтесь на какое-то время сохранить в памяти это изображение. Вскоре оно может оказаться полезным.
Чего-то не хватает в этом описании матрицы линейного преобразования. Действительно, может вызывать беспокойство тот факт, что мы, выработав математический аппарат, позволяющий выразить преобразования масштабирования, поворота и сдвига, а также любые комбинации этих преобразований, тем не менее, не можем с его помощью выразить простое преобразование перемещения.
Проблема заключается в том, что матрица 3×3 выражает линейное преобразование в трёхмерном пространстве, а перемещение — это попросту нелинейная функция. Например, представьте точки (1; 2; 3) и (3; 2; 1), которые могут быть также выражены векторами (1; 2; 3) и (3; 2; 1), исходящими из начала координат. (Я перехожу к векторам, чтобы придать смысл арифметическим операциям). Сложите эти два вектора, получив в результате вектор (4; 4; 4), и переместите его на одну единицу по оси X: получится (5; 4; 4). А теперь сперва произведите перемещение, получив в результате векторы (2; 2; 3) и (4; 2; 1), а затем сложите их. Сумма будет равна (6; 4; 4), что отличается от первого результата, наглядно показывая, что перемещение не является линейной функцией или линейным преобразованием.
Преобразования масштабирования, поворота и сдвига всегда производятся пропорционально по отношению к исходной фигуре. Неважно, насколько велика или мала фигура, — если она масштабируется с коэффициентом 2, она всегда удваивается в размерах. Иначе говоря, координаты точек фигуры в процессе преобразования умножаются на некоторый постоянный коэффициент. Однако перемещение математически производится иначе. Оно основано на сложении, а не на умножении. И поэтому в его основе лежат реальные единицы измерения, а не безразмерные коэффициенты.
Есть ли способ включить перемещение в удобную матрицу, разработанную нами для других типов преобразования?
Да, эта задача имеет решение, но оно не является интуитивно понятным. И, даже если вы знаете, как это делается, логика, стоящая за этим способам, может оказаться незнакомой вам.
Аффинные преобразования и выход за их пределы
Тот тип преобразований, к которому относятся перемещение, масштабирование, поворот и сдвиг, известен под именем аффинных преобразований. Слово «аффинный» происходит от латинского «affinis», означающего «родственный», но в математике оно обычно относится к чему-либо, остающемуся конечным, то есть конкретно определённым. Это значит, что аффинное преобразование никогда не преобразует точку, имеющие конечные координаты в трёхмерном пространстве, в точку, у которой хотя бы одна координата стала бы равна бесконечности. Конечно, это очень широкое определение, поэтому если говорить конкретно о преобразованиях, то аффинными среди них, в основном, являются все линейные преобразования, а также, в дополнение к ним, преобразование перемещения.
Поиск способа выражения аффинных преобразований в трёхмерном пространстве матричном виде будет существенно облегчен, если мы вернёмся в относительный комфорт двухмерного пространства.
Двухмерная аналогия
В двух измерениях (то есть на плоскости) линейные преобразования могут быть представлены матрицей 2×2:
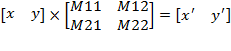
Формулы преобразования имеют следующий вид:
x' = M11 • x + M21 • y
y' = M12 • x + M22 • y
Эти формулы преобразования позволяют осуществлять масштабирование, поворот и сдвиг, но, как и формулы линейных преобразований в трёхмерном пространстве, не позволяют осуществлять перемещение. Ниже представлены три изображения небольшого двухмерного домика, помещённого в начало координат:
TwoDimensionalHouse.xaml
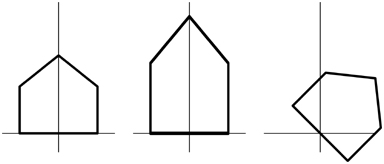
На втором изображении масштаб домика увеличен на 50% в направлении оси Y, а третье изображение представляет этот домик повёрнутым на 45 градусов по часовой стрелке вокруг начала координат. Но перемещение невозможно осуществить с помощью матрицы 2×2.
Этот двухмерный домик фактически идентичен передней грани (фасаду) трёхмерного домика, отображавшегося кодом из файла LinearTransformExperimenter.xaml. Единственное отличие заключается в том, что все координаты увеличены в 100 раз, поскольку такие величины лучше подходят для двухмерной системы координат WPF, базирующейся на разрешении 96 единиц на 1 дюйм.
Достаточно любопытно, но вы уже видели пример перемещения двухмерного домика. Фасад того трёхмерного домика, который мы рассматривали ранее в этой главе, и является этим двухмерным домиком. В последнем показанном мною примере сдвига, преобразование перемещает фасад домика в сторону от начала координат, но, при этом, не вносит никаких искажений в содержащую этот фасад плоскость:

Плоскость фасада этого трёхмерного домика, имеющая координату Z равную единице, таким образом фактически перемещается в сторону от начала координат на расстояние, определяемое коэффициентами сдвига, заданными в качестве элементов M31 и M32 матрицы преобразования:
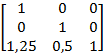
Из этой матрицы следуют следующие формулы преобразования:
x' = x + 1,25 z
y' = y + 0,5 z
z' = z
Но, если нас интересует только плоскость, у которой координата z равна 1, то формулы преобразования сократятся до формул перемещения по x и y:
x' = x + 1,25
y' = y + 0,5
Это серьёзное открытие: трёхмерный сдвиг, задаваемый элементами M31 и M32 матрицы преобразования, фактически перемещает двухмерные объекты по плоскости, координата z которой равна 1. Это — ключ к применению преобразования перемещения в двухмерной графике. Всегда, когда мы рисуем на плоскости, мы можем фактически представить это как рисование в трёхмерном пространстве. Концептуально это выглядит как изображение двухмерных фигур на плоскости, расположенной в трёхмерном пространстве, причём такой плоскости, что координаты z всех точек, образующих эту плоскость, были бы равны 1. На следующем рисунке эта плоскость показана в виде серой полупрозрачной поверхности:
2Don3D.xaml
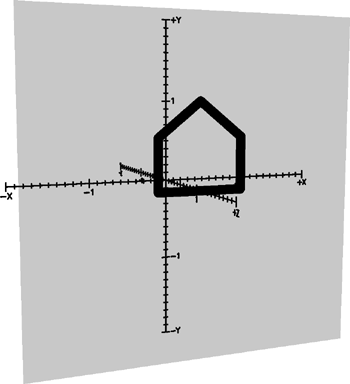
Поскольку теперь мы рисуем в трёхмерном пространстве, вместо оперирования точками с двухмерными координатами (x; y), мы фактически должны задавать точки с трёхмерными координатами (x; y; 1). Не запутайтесь: мы по-прежнему рисуем плоские фигуры на плоской поверхности. Три координаты точек в данном случае несут ту же информацию, что и две координатами. Но зато теперь мы можем применять трёхмерное преобразование сдвига для перемещения фигур по этой плоскости:
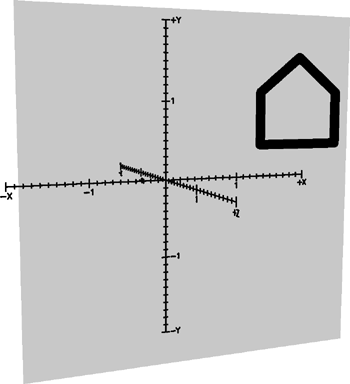
Конечно, на практике речь не идёт о том, чтобы на самом деле использовать трёхмерное пространство для рисования плоских фигур. Этот полностью воображаемый процесс. Всё, что нужно на само деле, — это расширенные возможности преобразования. Думаю, никто не удивится, узнав, что обычная структура Matrix, определённая в пространстве имён System.Windows.Media, обслуживающая двухмерную графику в WPF, фактически реализует матрицу 3×3 и имеет следующие свойства:
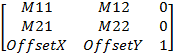
Концептуально, для целей умножения матриц, все точки с координатами (x; y) представляются в виде (x; y; 1):
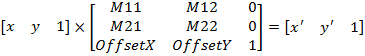
Формулы преобразования имеют вид:
x' = M11 • x + M21 • y + OffsetX
y' = M12 • x + M22 • y + OffsetY
Подведём итоги: чтобы задействовать преобразование перемещения в двухмерной графике, необходимо использовать матрицу линейных преобразований для трёхмерного пространства. Этот приём станет очевидным, как только вы осознаете, что трёхмерный сдвиг в направлении X и Y эквивалентен двухмерному перемещению на плоскости, параллельной (но не равной) координатной плоскости XY. Чтобы упростить вычисления, в качестве такой плоскости обычно выбирают ту, для которой координата z равна 1, а все, принадлежащие ей точки имеют координаты вида (x; y; 1). Множество двухмерных преобразований, которые становится возможным описать с помощью этой увеличенной матрицы, известно под названием «аффинных преобразований» и является расширением множества линейных преобразований.
Что можно сказать о третьем столбце этой матрицы 3×3? При использовании подобной матрицы линейных преобразований третьего порядка в мире трёхмерных координат этот столбец применяется при масштабировании в направлении оси Z или же при вращении вокруг чего-либо за исключением оси Z. Но в двухмерной графике этот столбец, кажется, не несёт никакой полезной нагрузки.
На самом деле, двухмерная графическая система WPF не даст вам возможности работать с элементами третьего столбца объекта Matrix. Но теоретически, вы можете думать об этом столбце как о дополнительных, своего рода «бонусных», ячейках. И, если бы вы могли задавать этим элементам любые другие значения, отличные от заданных по умолчанию 0, 0 и 1, то таким образом вы бы смогли описать преобразование, которое было бы не только нелинейным, но также и неаффинным.
Давайте на миг представим, что у нас есть возможность задавать значения элементов третьего столбца матрицы и что двухмерное преобразование на самом деле выглядит так:
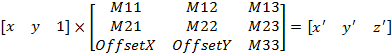
В этом случае формулы преобразования примут вид:
x' =M11 • x + M21 • y + OffsetX
y' =M12 • x + M22 • y + OffsetY
z' =M13 • x + M23 • y + M33
Если значения в третьем столбце матрицы не равны 0, 0 и 1 соответственно, то в результате преобразования точка уйдёт за пределы плоскости, в которой координата z равна 1. А поскольку в этом примере мы всё ещё продолжаем работать с двухмерной графикой, нам придётся как-то вернуть преобразованную точку обратно на плоскость. Нам надо найти способ изменит значения x', y' и z' так, чтобы координата Z снова стала равна 1, и фигура разместилась бы на плоскости.
Простейшим решением будет поделить все три координаты на z':
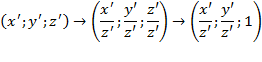
Теперь мы снова имеем точку на плоскости, у которой координата z равна 1. Однако мы привнесли возможность весьма опасного исхода: деление, применённое в этой операции, вполне может оказаться делением на ноль. Это означает, что в результате преобразования координата точки может стать равной бесконечности. Именно возможность получить в результате бесконечность делает это преобразование неаффинным. Ведь по определению, аффинные преобразования — это те, в результате которых координаты не обращаются в бесконечность.
Этот конкретный вид неаффинных преобразований, который я здесь описываю, иногда называют конусным преобразованием, поскольку оно не сохраняет параллельность линий и, вместо этого, сужает фигуру с одной стороны и расширяет с другой. Например, рассмотрим следующую двухмерную матрицу неаффинного преобразования:
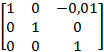
Значение элемента M13 равное –0,01 представляется незначительным, но оно оказывает большое влияние на двухмерную графику в координатной системе, основанной на разрешении 96 единиц на дюйм. Формулы преобразования выглядят так:
x' = x
y' = y
z' = 1 – 0.01x
Точка (x; y) переходит в следующую точку:
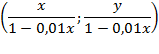
Когда x равен 100, знаменатель дроби обращается в ноль, а координата становится равной бесконечности. К счастью, значения абсцисс точек маленького двухмерного домика ограничены интервалом от –50 до 50, то есть знаменатель принимает значения от 1,5 до 0,5. Вот как выглядит преобразованная версия домика:
TaperTransformedHouse.xaml
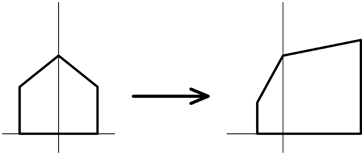
Часть фигуры, расположенная правее начала координат стала больше, так как увеличились значения координат составляющих её точек, в то время как часть фигуры, расположенная слева от начала координат, по той же причине стала меньше. Если это хоть как-то напоминает эффект перспективы, то вы, кончено, уже предполагаете, как можно использовать эту схожесть.
Когда вы создаёте представление для точки с двухмерными координатами (x; y) при помощи дополнительной третьей координаты, вы используете концепцию однородных координат, разработанную немецким математиком Августом Фердинандом Мёбиусом (1790–1868), наиболее известным сегодня в связи с топологическим парадоксом, называемом петля Мёбиуса. В трёхмерном пространстве однородные координаты полезны не только для выражения перемещений, но также играют важную роль в описании перспективы.
Трёхмерные однородные координаты
Продолжение следует...
Перевод: Андрей Мурзин