
Перевод записи из блога Чарльза Петцольда (Charles Petzold).
Ссылка на оригинал: Non-Affine Transforms in 2D?
Недавно на форуме MSDN, посвящённом WPF, спросили, возможно ли применить неаффинное преобразование для двумерной графики. Простой ответ — «нет». Структура Matrix (определённая в пространстве имён System.Windows.Media), описывающая матрицу 3×3, не позволяет задавать значения для третьего столбца этой матрицы, что позволило бы совершать неафинные преобразования.
Тем не менее, неаффинные преобразования допустимы в WPF (в той его части, которая предназначена для работы с трёхмерной графикой) и, кроме того, необходимый эффект можно получить и не связываясь с преобразованиями вообще.
Здесь представлены две программы, каждая из которых отображает квадрат с моей фотографией. С помощью мыши вы можете захватить любой из углов квадрата и потянуть за него. Щёлкать мышью надо внутри изображения! Ближайший к месту щелчка угол передвинется в место нахождения курсора мыши, и затем вы можете перетащить этот угол в другое место. Пока вы перетаскиваете один угол, другие остаются неподвижными. Вот ссылка на первую программу:
Примечание: Ссылка на XBAP — браузерное приложение XAML. Может быть запущено в Microsoft Internet Explorer, а также (при наличии плагина) в Mozilla Firefox. В последних версиях браузеров запуск таких приложений по умолчанию запрещён в целях безопасности.
Для разрешения запуска в Internet Explorer (версия 9):
Сервис → Свойства обозревателя → Безопасность → Другой… → XAML-приложения веб-обозревателя → Включить
Здесь применён простой подход: используется подмножество типов WPF для работы с трёхмерной графикой (WPF 3D) для отображения квадрата, помещённого на координатную плоскость XY. В коллекции Positions (позиции) экземпляра класса MeshGeometry3D (трёхмерная геометрия типа сетки) заданы следующие координаты точек в трёхмерном пространстве: (0; 0; 0), (0; 1; 0), (1; 0; 0) и (1; 1; 0). Всякий раз, когда на изображении производится щелчок мышью или совершается перетаскивание мышью, программа запрашивает двухмерные координаты указателя мыши, преобразует их в трёхмерные и изменяет соответствующий элемент в коллекции Positions. Преобразование координат производится при помощи простого метода, который работает только с камерой ортогональной проекции (объектом типа OrthographicCamera), направленной прямо вдоль оси Z. Исходный код этого решения доступен для загрузки.
Проблема этого метода заключается в том, что в нём исходное квадратное изображение делится по диагонали на два треугольника: один в левой нижней части, а другой — в правой верхней. И, если вы перетаскиваете левый нижний или правый верхний угол, то растягивается только половина изображения, как показано на рисунке:

На рисунке можно, практически, увидеть диагональ, проходящую из левого верхнего угла в правый нижний. Какие-либо искажения изображения ниже этой линии отсутствуют.
Наверное, лучшим подходом к решению задачи явилось бы применение настоящего неаффинного преобразования к объекту типа GeometryModel3D (модель трёхмерной геометрии). Это делается в следующей программе:
Примечание: Ссылка на XBAP — браузерное приложение XAML. Может быть запущено в Microsoft Internet Explorer, а также (при наличии плагина) в Mozilla Firefox. В последних версиях браузеров запуск таких приложений по умолчанию запрещён в целях безопасности.
Для разрешения запуска в Internet Explorer (версия 9):
Сервис → Свойства обозревателя → Безопасность → Другой… → XAML-приложения веб-обозревателя → Включить
Да, здесь тоже есть проблема: можно легко перетащить угол изображения в такое место, где ожидаемого преобразования не происходит, а изображение странным образом переворачивается. Но, как вы можете видеть, при перемещении любого угла, всякий раз преобразование затрагивает всё изображение целиком:

Исходный код для этой второй версии также доступен для загрузки. В целях нижеследующего теоретического разбора я буду предполагать, что мы работаем только с двумя измерениями. В трёхмерном пространстве достаточно тривиально перейти к работе на плоскости, приняв координату Z равной 0.
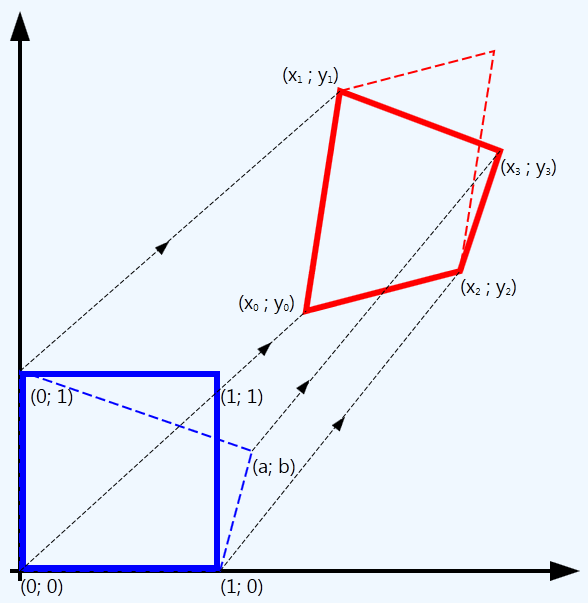
Нам нужно преобразование, производящее следующие переходы (я надеюсь, что вы видите стрелки между парами точек):
(0; 0) → (x0; y0)
(0; 1) → (x1; y1)
(1; 0) → (x2; y2)
(1; 1) → (x3; y3)
Координаты в левой части каждой строки являются координатами углов исходного изображения. Координаты в правой части задают четыре точки, в которые мы хотим переместить эти углы. Вообще, так описывается неаффинное преобразование: оно отображает квадрат в произвольный четырёхугольник. Аффинные преобразования всегда превращают квадраты в параллелограммы. Желаемое нами преобразование будет намного легче получить, если мы разобьём его на два преобразования:
(0; 0) → (0; 0) → (x0; y0)
(0; 1) → (0; 1) → (x1; y1)
(1; 0) → (1; 0) → (x2; y2)
(1; 1) → (a; b) → (x3; y3)
Первое преобразование, которое я буду называть B, очевидно, является неаффинным. Второе преобразование, которое я постараюсь сделать аффинным, пусть называется A (от слова «аффинный»). Итоговое суммарное преобразование является их произведением: B×A. Итак, здесь нам требуется найти параметры этих двух преобразований, а также координаты точки (a, b). Давайте начнём с того, что построим аффинное преобразование.
Аффинное преобразование всегда превращает квадрат в параллелограмм, поэтому оно полностью определяется сопоставлением трёх точек. Я буду использовать первые три в списке:
(0; 0) → (x0; y0)
(0; 1) → (x1; y1)
(1; 0) → (x2; y2)
Матрица (3×3) для аффинного преобразования может быть представлена следующим образом (используя имена свойств упомянутой структуры Matrix):
| M11 | M12 | 0 |
| M21 | M22 | 0 |
| OffsetX | OffsetY | 1 |
Формулы преобразования выглядят так:
x' = M11•x + M21•y + OffsetX
y' = M12•x + M22•y + OffsetY
Достаточно легко применить преобразование к точкам (0; 0), (0; 1) и (1; 0) и вычислить элементы матрицы:
M11 = x2 – x0
M12 = y2 – y0
M21 = x1 – x0
M22 = y1 – y0
OffsetX = x0
OffsetY = y0
Хотя знать это и необязательно, но четвёртая вершина квадрата — та, которая с координатами (1; 1), — при этом преобразовании перешла бы в точку с координатами (M11 + M21 + OffsetX; M12 + M22 + OffsetY), являющуюся четвёртой вершиной параллелограмма. Но в этом упражнении нам важна не эта точка, а некоторая точка (a, b), которая в результате этого аффинного преобразования переместится в точку (x3, y3). Но что это за точка (a, b)? Применим к её координатам формулы аффинного преобразования и найдём значения a и b:
a = (M22•x3 – M21•y3 + M21•OffsetY – M22•OffsetX) / (M11•M22 – M12•M21)
b = (M11•y3 – M12•x3 + M12•OffsetX – M11•OffsetY) / (M11•M22 – M12•M21)
Теперь давайте обратим внимание на неаффинное преобразование, в результате которого произошли бы следующие превращения:
(0, 0) → (0, 0)
(0, 1) → (0, 1)
(1, 0) → (1, 0)
(1, 1) → (a, b)
В общем виде матрицу неаффинного преобразования можно записать так (используя и те имена свойств, которые не определены в упоминавшейся структуре Matrix):
| M11 | M12 | M13 |
| M21 | M22 | M23 |
| OffsetX | OffsetY | M33 |
А формулы преобразования выглядят так:
x' = (M11•x + M21•y + OffsetX) / (M13•x + M23•y + M33)
y' = (M12•x + M22•y + OffsetY) / (M13•x + M23•y + M33)
Итак, попробуем вычислить эти параметры для нашего неаффинного преобразования.
Точке (0; 0) в результате преобразования соответствует точка (0; 0). Это говорит нам о том, что параметры OffsetX и OffsetY равны нулю, а параметр M33 не равен нулю. Рискнём предположить, что параметр M33 равен 1.
Точке (0; 1) в результате преобразования соответствует точка (0; 1). Это говорит нам о том, что параметр M21 равен нулю, а M23 = M22 – 1.
Точке (1; 0) в результате преобразования соответствует точка (1; 0). Это говорит нам о том, что параметр M12 равен нулю, а M13 = M11 – 1.
Точка (1; 1) должна перейти в точку (a, b). В результате несложных алгебраических преобразований получим следующее:
M11 = a / (a + b – 1)
M22 = b / (a + b – 1)
Значения a и b уже были вычислены на этапе разбора аффинного преобразования.
Вычисления матрицы аффинного преобразования A и матрицы неаффинного преобразования B реализованы в методе CalculateNonAffineTransform (рассчитать неаффинное преобразование) в файле «NonAffineImageTransform2.cs». Разумеется, метод на самом деле возвращает объект типа Matrix3D, который применяется к объекту типа GeometryModel3D, содержащему изображение.
Использование трёхмерной графики для реализации двухмерных неаффинных преобразований может показаться несколько экстравагантным, но всё же имейте в виду, что Viewport3D является таким же элементом управления WPF, как и любой другой. Вы можете легко сочетать его с панелями, элементами TextBlock, другими элементами управления и всем прочим. В частности, можно проводить преобразования между двумя системами координат, легко рассчитав необходимый размер окна просмотра Viewport3D в зависимости от размера предметов, изображение которых получается с помощью камеры ортогональной проекции (OrthographicCamera).
Чарльз Петцольд (Charles Petzold) — программист, автор технической литературы по компьютерной тематике (более 10 книг, множество статей, блог).
Популяризатор Microsoft Windows.
С 1985 по 2000 год — редактор журнала Microsoft Systems Journal. Его статья, опубликованная в декабре 1986 года во втором номере этого журнала, считается первой статьёй о программировании для Windows.
Перевод: Андрей Мурзин